Idea Development: Part I

“PUZZLES AND FUN”

The learning activity for this week consists of three parts, or “questions”.

The first part is a series of riddles or puzzles, the second is an analysis of the fast-food chain McDonald’s, using the SCAMPER method, and the third is to apply the SCAMPER method to modify or improve two existing objects.
This journal entry will focus on the first part: PUZZLES AND FUN.

Question 1:

A man is replacing a wheel on his car, when he accidentally drops the four nuts used to hold the wheel on the car. They fall into a deep drain, irretrievably lost. A passing girl offers him a solution that enables him to drive home. What is it?

Answer:

• The girl can tell the man to take a nut from each of the other three wheels and use them as temporary replacements. It wouldn’t be safe to use the car over longer distances, but he can at least drive home or a store with spare parts.
• Another solution would be that the girl happens to be his wife, and she offers him to drive her car home.
• She could be offering to tow his car home, but she feels uncomfortable doing it, so he can drive the car home.

Question 2:

Two Russians walk down a street in Moscow. One Russian is the father of the other Russian’s son. How are they related?

Answer:

• The most likely answer: They are the son’s parents, and the other Russian is the mother.
• The Russian has adopted the other Russian’s son.

Question 3:

What occurs once in June, once in July and twice in August?

Answer:

• The letter U can be found once in June, once in July and twice in August.

Question 4:

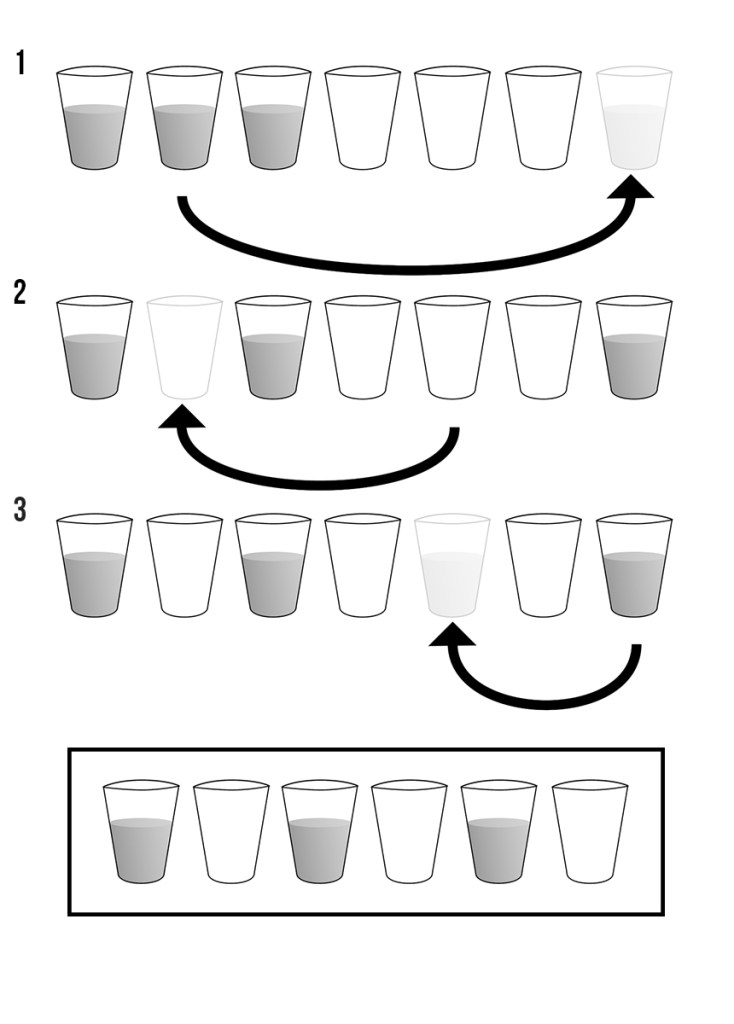
Six drinking glasses stand in a row, with the first three full of water and the next three empty. By handling and moving only one glass at a time, how can you arrange the six glasses so that no full glass stands next to another full glass, and no empty glass stands next to another empty glass? What is the minimum number of moves to solve this puzzle?

Answer:

Considering that the question specifies the word “arrange”, I assume that means I have to move the glasses like in a logical puzzle, which requires three moves (otherwise I would pour a little from glass number 2 into glass number 4 and 6, which would require just one move):

First move glass number 2 to the opposite end of the row. Then move the secondmost glass from the right, into the empty space, where glass number 2 used to be. Place the first glass you moved, glass number 2, into the empty spot, where the empty glass used to be. That was three moves.